Parallax Rooms
The idea
On my city builder project, I wanted the buildings to show rooms behind the windows. However adding all the geometry for such a large amount of rooms would have killed my machine, even with instancing. Luckily there exists an idea to fake all the rooms, although there are some restrictions. For example all rooms must be rectangular, there’s less architectural freedom in the allowed design. However this usually is not a big issue, since a normal room is rectangular. Basically what we need to do is to perform a local ray-box intersection within the shader.

We need to modify the texture coordinate of the currently shaded sample in a manner, that it appears to be a room. As input we receive the uv coordinate of the window plane and the direction from the camera. We then construct a virtual box and trace the ray through the pixel of the window face onto the 5 remaining sides of the box. This will result in a point marked above as P. This point is lying on one of the possible 5 sides A-E (we exclude the front side of the box).

In theory, we could take the coordinate of the side being hit and depending on its orientation drop one coordinate. This coordinate could be used as the uv coordinate into a flat image of the respective wall. It would be quite easy, but we would need 5 textures per room. We want to achieve the same result with a single texture, preferably originating from either a direct photo of a room or a rendering of a virtual room. Like this one:

To achieve this, we need to perform a mapping of the rectangular area of the wall into a trapezoidal area on the used texture. So The basic idea of the shader is the following:
Input: Front-side-uv & view direction & face normal
==>
Ray box intersection
==>
UV on wall & wall id
==>
Trapezoidal transform
==>
UV on intended texture
Parameterization
In order to map the room from a single texture, we need to pass in some information about the room geometry into the custom shading node. These are:
- Depth of the room.
- Texture inset: This specifies the perspective of the camera used to shoot the image of the mapped room.
- Aspect ratio: Specifies if the room is square or rectangular.
Further parameters of the custom shading node are
- Number of rooms: Maps each random room to a different UDIM tile. That way, we can render different rooms by a single texture look-up.
- Seed: To randomize the distribution of the chosen random rooms, the seed can be driven from the outside.
- Enable Random per Island: If turned off, room randomization happens per object, otherwise per texture island. If disabled, one object can be used to model multiple windows into the same room. If enabled, a complete house can be modeled as one single mesh and have each UV island represent a window into a different room.
Input: Coordinate system construction
In order to perform a simple ray box intersection, we need to transform the given information into an axis aligned system. Our intention is, that the room will occupy the [0:1]³ space:
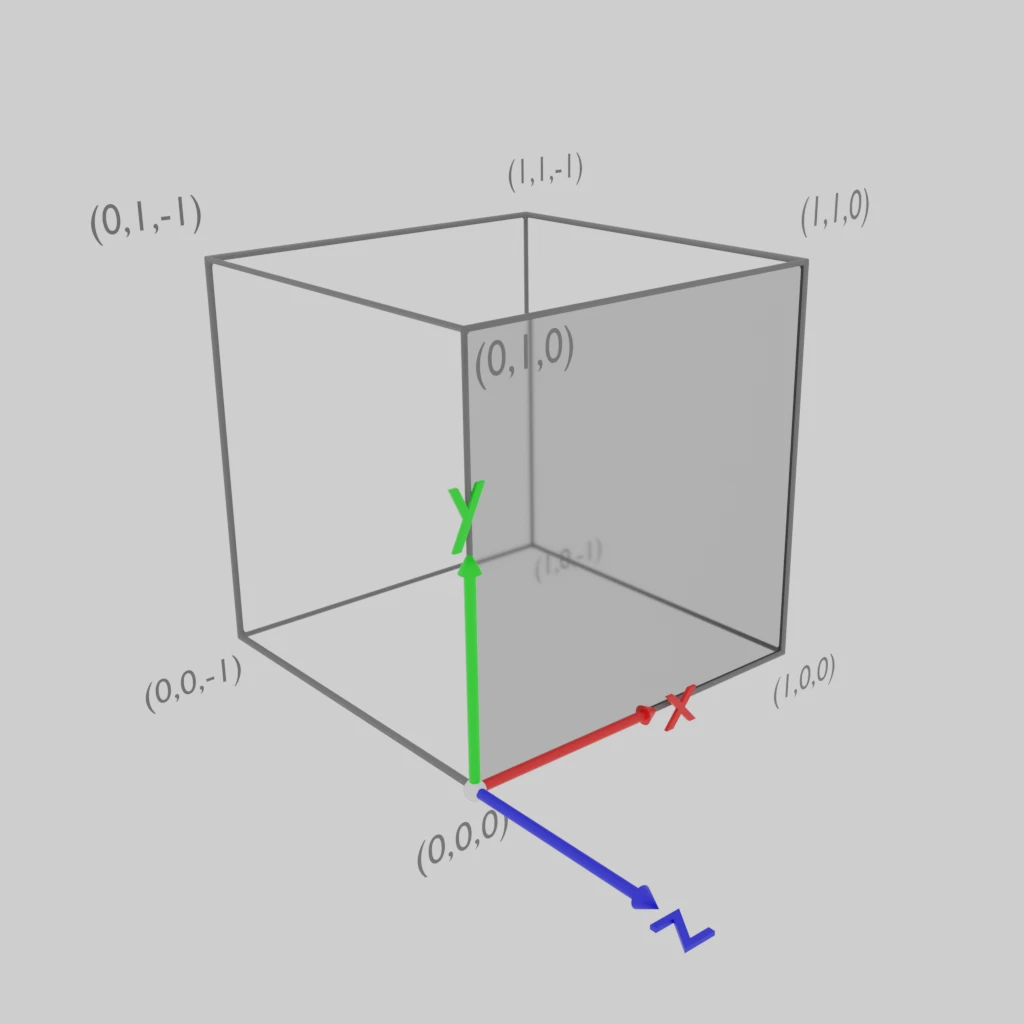
The milky face on the front of the box is the face, that gets rendered. We span the room to the back of the uv coordinate space. This means, if we texture the face on the whole [0:1]² uv space, we see the full room. If we place the uvs on a smaller range, we can model a window.
Our goal in this step is to transform the ray direction into uv-space. This in done the following way:
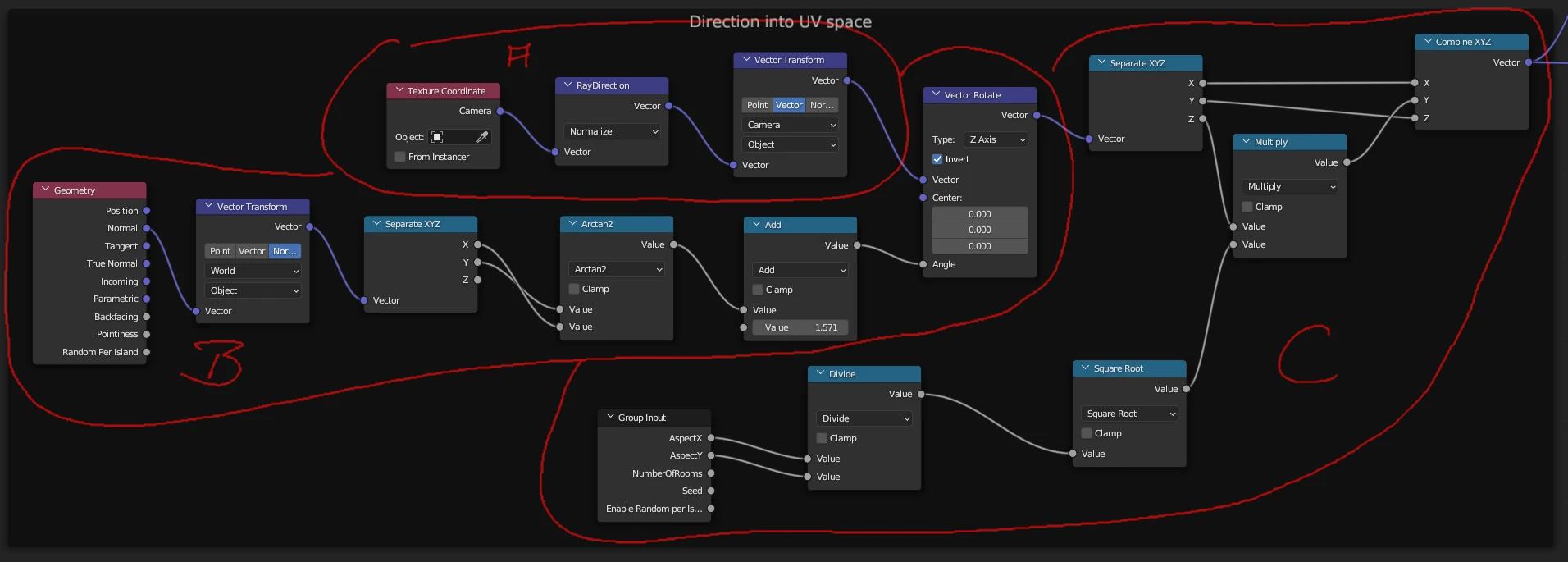
Computation is split into 3 main calculations. First in section A, we transform the ray direction from camera space into object space. However, our windows might not be aligned with the xz-plane in object space, that’s why we need to rotate the calculated vector to the alignment of the face itself. We assume the windows are vertically aligned (normal vector’s z-component is zero). This leads is to section B. Here we take the normal vector (given in world space), transform it to object space and through the atan2 function calculate the angle the face is rotated around the z-axis. However the angle we compute here is measured starting from the x-axis, but we want our y-axis to point into the room. So we need to add π/2 in order to achieve this. The computed angle is then used to Vector Rotate the ray direction from step A. The last section C is used to transform the direction, such that the room mapped to the square can represent an arbitrary aspect ratio. Additionally here coordinates are swizzled such that x and y of the direction are aligned with the u and v coordinates and z represents the depth. This allows to interpret the point (u,v,0) as the origin of the ray, we want to intersect with the box.
Ray box intersection
Ray box intersection is divided into 5 ray plane intersections. This is done according to the following formula. Given the following variables:
\[\begin{aligned} \mathbf{p_0}& \text{: Origin of the ray} \\ \mathbf{d} & \text{: Direction of the ray} \\ t & \text{: Parameter of the ray} \\ \mathbf{o} & \text{: Origin of the plane } \\ \mathbf{n} & \text{: Normal of the plane } \end{aligned}\]We can define a ray as:
\[Ray(t) = \mathbf{p_0}+t\mathbf{d}\]The plane can be implicitly defined through its origin point and a normal vector:
\[(x-o) \cdot n = 0\]Replacing x with the ray’s formula, we can solve for the variable \(t\):
\[t={({\mathbf{o}}-{\mathbf {p_{0}}})\cdot {\mathbf {n}} \over {\mathbf {d}} \cdot {\mathbf {n}}}.\]Since we aligned our ray to the uv space of the face, we only have to deal with 5 very simple planes:
| Nr. | Origin | Normal |
|---|---|---|
| 1 | (0,0, 0) | ( 1, 0,0) |
| 2 | (0,0, 0) | ( 0, 1,0) |
| 3 | (1,0, 0) | (-1, 0,0) |
| 4 | (0,1, 0) | ( 0,-1,0) |
| 5 | (0,0,-1) | ( 0, 0,1) |
This facilitates the intersection formula from above quite drastically, since calculating the dot product with the normal vector of the plane will be reduced to extracting the right coordinate and maybe negating the value. This is done in the following section of the shading network:
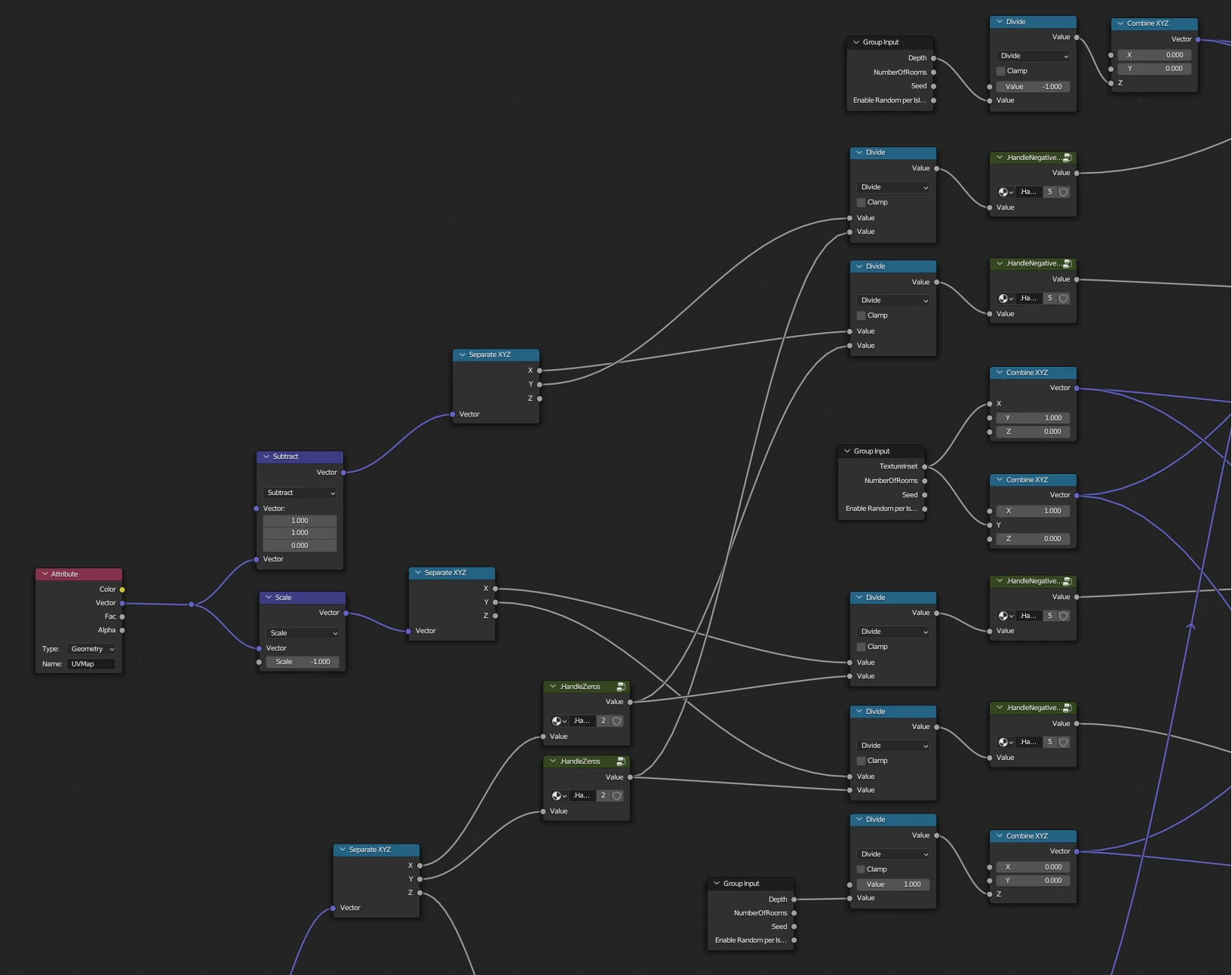
As one can see, the shading network spreads out and in principle calculates the 5 ray plane intersections in parallel. Now we just need to search for the plane with the smallest parameter t. But we need to treat one specific situation and that’s the one, the ray hits one of the planes behind its starting point. Since the ray starts on the window face, a hit behind the start point would lie outside of the building. We can recognize those situations easily with parameters of \(t<0\). To unify the remaining logic, the shader detects a value of \(t<0\) and adds a very large value to it, thus making it positive again. The resulting point on the ray will lie so far away from the origin, that that it will definitely not being selected, since a hit point from another wall will definitely be closer. The following video illustrates that process:
The selection of the ray with the closest hit point is done with a very simple node group. It takes the information of 2 rays - the hit point parameter \(t\) and the computed uv coordinate (see next section).
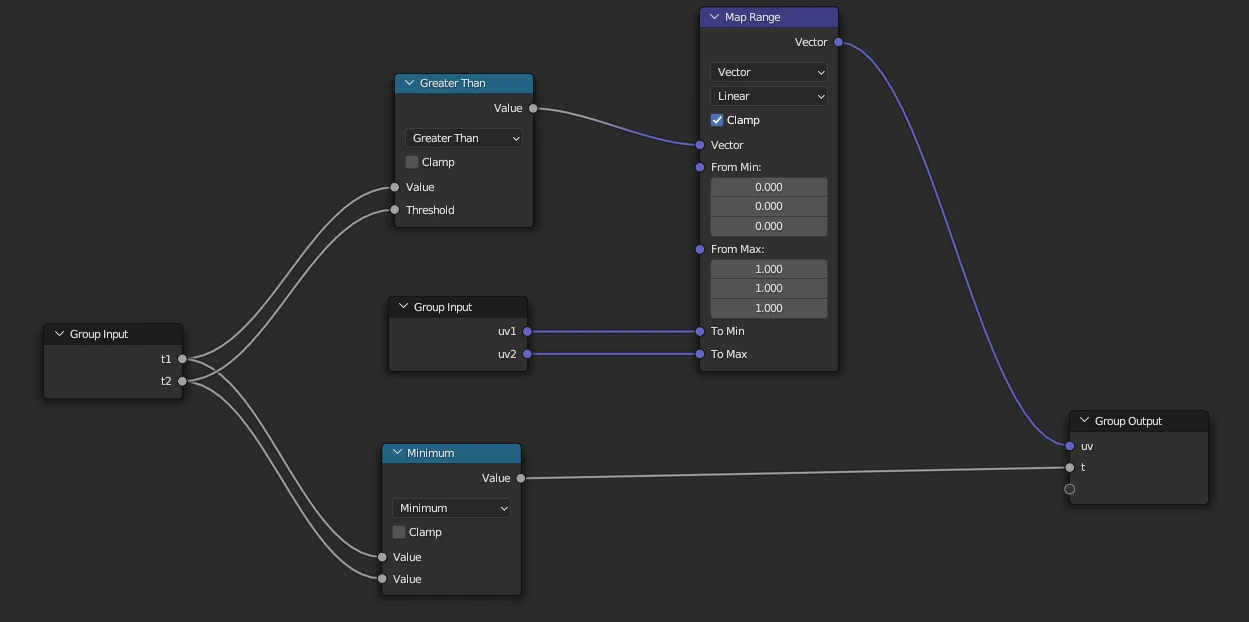
The shading group compares the parameters \(t\) and utilizes a MapRange node to switch between the respective uv coordinates. Output is again both parameters of a ray \(t\) and \(uv\). That way, we combine step-by-step 2 rays until the shortest one is left over.
Trapezoidal transform
When a hit point on a box side was found, it is needed to compute a uv texture coordinate for that point. This is done by parametrizing the rendered room in uv space. The used images show the room looking along the central axis. This means, we have a vanishing point in the center of the image. Depending on the depth of the room and the focal length of the camera, the back wall will occupy a certain rectangle inset from the image. This inset and the aspect ratio of the room are the two parameters we need to describe the layout of the 5 walls inside of the texture space. The ceiling, floor and the 2 side walls are perspectively distorted in the used texture (sections A,C,D and E on the image above). Luckily, because we render the source texture straight centered into the room, those sections are trapezoids. We can easily, from the hit point of the ray, get a u’v’ coordinate like if the wall image was projected flat. Now we need to transform the u’v’ into the real uv. This is done like this:
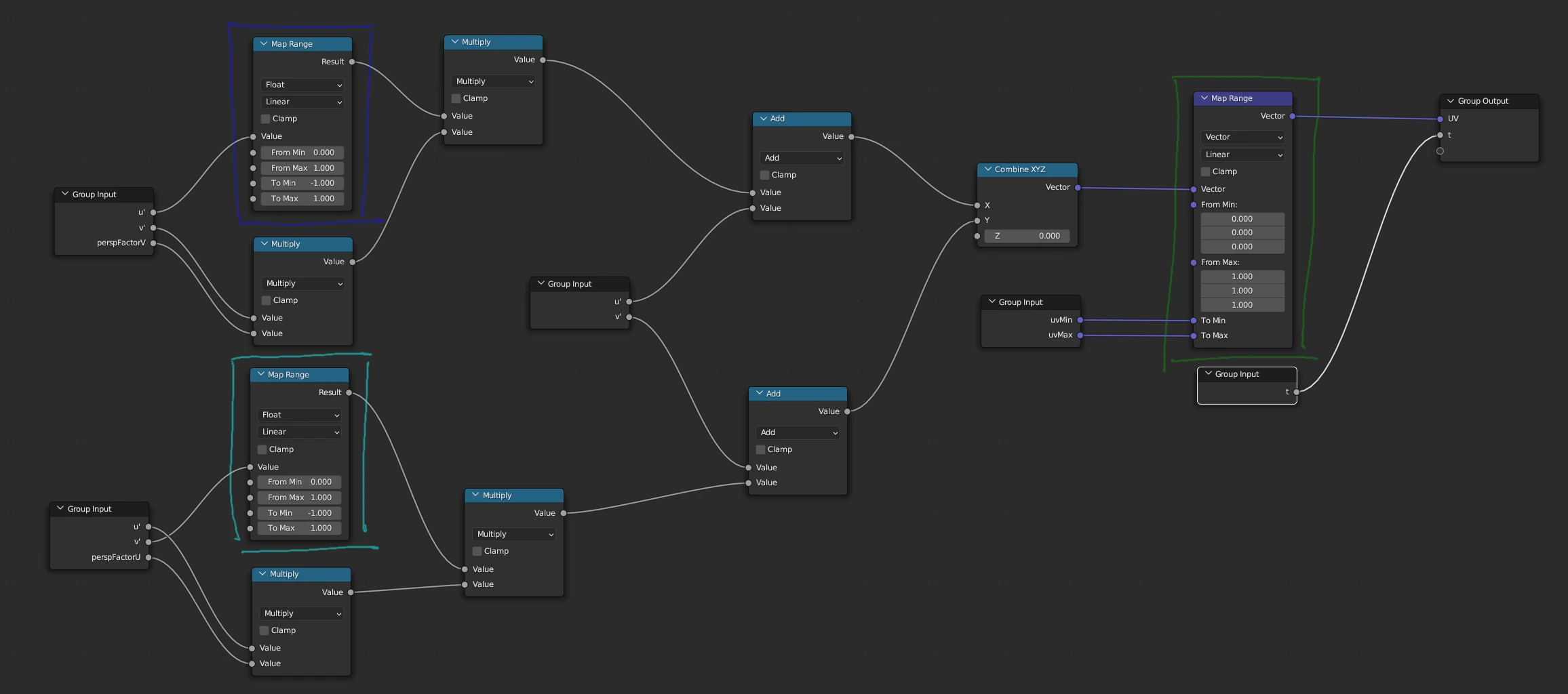
This utility subgraph has a couple of input parameters. The u’v’ texture coordinates of the hit point. Perspective factors in u and v direction. This describes the incline of the trapezoid (which is dependent on the aspect ratio of the image). and the uv bounding box, the trapezoid occupies in the used image (calculated from the inset factor).
\[\begin{aligned} p_u & \text{: perspective factor in u direction (incline of trapezoid)} \\ p_v & \text{: perspective factor in v direction (incline of trapezoid)} \\ u_{min} & \text{: minimum of bounding box in final uv space} \\ u_{max} & \text{: maxmimum of bounding box in final uv space} \\ v_{min} & \text{: minimum of bounding box in final uv space} \\ v_{max} & \text{: maxmimum of bounding box in final uv space} \\ u' & \text{: u texture coordinate planar to the wall } \\ v' & \text{: v texture coordinate planar to the wall } \\ u & \text{: u texture coordinate inside the used image } \\ v & \text{: v texture coordinate inside the used image } \end{aligned}\] \[\begin{aligned} u&=({u' + {\color{blue}2}{p_v}v'{\color{blue}(u'-0.5)}})\color{green}(u_{max}-u_{min})+u_{min} \\ v&=({v' + {\color{cyan}2}{p_u}u'{\color{cyan}(v'-0.5)}})\color{green}(v_{max}-v_{min})+v_{min} \end{aligned}\]One of the perspective factors is always 0, since we deal with axis aligned trapezoids. However to make the node group applicable to all walls, the floor and the ceiling, we can feed in both, depending on the orientation of the needed trapezoid.
The colored parts of the formula are realized through mapRange nodes in the shader graph. Those are highlighted in the respective colors of the screenshot.
Try it out yourself
The node group described here is available in my GitLab node repository. Feel free to download and try the demo scene yourself. Just make sure, you also grab the example textures in the subfolder rooms, in case you don’t clone the whole repository. Happy rendering.